DEEP NEURAL NETWORK-BASED APPROACH FOR COMPUTING SINGULAR VALUES OF MATRICES
DOI:
https://doi.org/10.25271/sjuoz.2025.13.1.1345Keywords:
Singular Value Decomposition, Matrix Factorization, Convolutional Neural Networks, Computational CompelxityAbstract
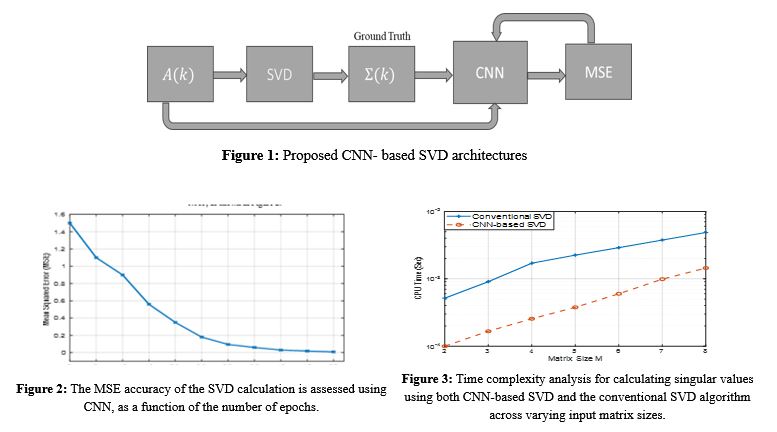
Matrix factorization techniques, such as Singular Value Decomposition (SVD), Eigenvalue Decomposition (EVD), and QR decomposition, have long been pivotal in computational mathematics, particularly for applications in signal processing, machine learning, and data analysis. With the growing size and complexity of data, traditional methods of matrix factorization face challenges in efficiency and scalability. This paper investigates the implementation of Convolutional Neural Networks (CNNs) for computing the singular values of both real and complex matrices. By leveraging the hierarchical feature extraction capabilities of CNNs, this approach aims to enhance the accuracy, efficiency, and scalability of SVD calculations. The proposed CNN-based SVD method is evaluated against the conventional SVD algorithm, demonstrating superior performance in terms of computational time and accuracy.
References
Albawi, S., Bayat, O., Al-Azawi, S., & Ucan, O. N. (2018). Social touch gesture recognition using convolutional neural network. Computational Intelligence and Neuroscience,2018(1),6973103.DOI:https://doi.org/10.1155/2018/6973103
Anwar, S. M., Majid, M., Qayyum, A., Awais, M., Alnowami, M., & Khan, M. K. (2018). Medical image analysis using convolutional neural networks: a review. Journal of medicalsystems,42,1-13.DOI: https://doi.org/10.1007/s10916-018-1088-1
Finol, D., Lu, Y., Mahadevan, V., & Srivastava, A. (2019). Deep convolutional neural networks for eigenvalue problems in mechanics. International Journal for Numerical Methods in Engineering, 118(5), 258-275. DOI: https://doi.org/10.1002/nme.6012
Golub, G. H., & Van Loan, C. F. (2013). Matrix computations. JHUpress.DOI: https://doi.org/10.1137/1.9781421407944
Han, J., Lu, J., & Zhou, M. (2020). Solving high-dimensional eigenvalue problems using deep neural networks: A diffusion Monte Carlo like approach. Journal of ComputationalPhysics,423,109792.DOI: https://doi.org/10.1016/j.jcp.2020.109792
Hang, T., Yang, G., Yu, B., Liang, X., & Tang, Y. (2013). Neural network based algorithm for generalized eigenvalue problem. In 2013 International Conference on Information Science and Cloud Computing Companion (pp.446-451).IEEE.DOI: https://doi.org/10.1109/ISCC-C.2013.93
Hogben, L. (Ed.). (2006). Handbook of linear algebra. CRC press. DOI: https://doi.org/10.1201/9781420010572
Hassan, M. M., & Taher, S. A. (2022). Analysis and classification ofautismdata using machine learning algorithms. Science Journal of University of Zakho, 10(4),206-212.DOI: https://doi.org/10.25271/sjuoz.2022.10.4.1036
Hsia, S. C., Wang, S. H., & Chang, C. Y. (2021). Convolution neural network with low operation FLOPS and high accuracy for image recognition. Journal of Real-Time Image Processing, 18(4), 1309-1319 DOI: https://doi.org/10.1007/s11554-021-01140-9
Hsu, C. H., & Kremer, U. (2003). The design, implementation, and evaluation of a compiler algorithm for CPU energy reduction. In Proceedings of the ACM SIGPLAN 2003 conference on Programming language design and implementation(pp.38-48).DOI: https://doi.org/10.1145/781131.781137
Hu, Z. (2022). Estimation and application of matrix eigenvalues based on deep neural network. Journal of Intelligent Systems,31(1),1246-1261.DOI: https://doi.org/10.1515/jisys-2022-0126
LeCun, Y. (1998). The MNIST database of handwritten digits. http://yann. lecun. com/exdb/mnist/.
Li, Z., Liu, F., Yang, W., Peng, S., & Zhou, J. (2021). A survey of convolutional neural networks: analysis, applications, and prospects. IEEE transactions on neural networks and learning systems, 33(12), 6999-7019. DOI: 10.1109/TNNLS.2021.3084827
Mala, Y. H., & Mohammad, M. A. (2022). Brain Waves Signal Modeling for Object Classification Using Random Forest Method. Science Journal of University of Zakho, 10(1), 16-23. DOI:https://doi.org/10.25271/sjuoz.2022.10.1.876
Nguyen, D. M., Tsiligianni, E., & Deligiannis, N. (2018). Matrix factorization via deep learning. arXiv preprint arXiv:1812.01478.DOI:https://doi.org/10.48550/arXiv.1812.01478
Rawat, W., & Wang, Z. (2017). Deep convolutional neural networks for image classification: A comprehensive review. Neural computation, 29(9), 2352-2449. DOI: 10.1162/neco_a_00990
Strang, G. (2022). Introduction to linear algebra. Wellesley-Cambridge Press. DOI: 10.4236/jamp.2020.87104
Wu, C. H., & Tsai, P. Y. (2019). An SVD processor based on Golub–Reinsch algorithm for MIMO precoding with adjustable precision. IEEE Transactions on Circuits and Systems I: Regular Papers, 66(7), 2572-2583. DOI: 10.1109/TCSI.2019.2899211
Yi, Z., Fu, Y., & Tang, H. J. (2004). Neural networks based approach for computing eigenvectors and eigenvalues of symmetric matrix. Computers & Mathematics with Applications,47(8-9),1155-1164.DOI:https://doi.org/10.1016/S0898-1221(04)90110-1
Zhang, X. D. (2017). Matrix analysis and applications. CambridgeUniversityPress.DOI:https://doi.org/10.1017/9781108277587
Zou, X., Tang, Y., Bu, S., Luo, Z., & Zhong, S. (2013). Neural-network-based approach for extracting eigenvectors and eigenvalues of real normal matrices and some extension to real matrices. Journal of Applied Mathematics, 2013. DOI:https://doi.org/10.1155/2013/597628
Published
How to Cite
Issue
Section
License
Copyright (c) 2025 Diyari A. Hassan
This work is licensed under a Creative Commons Attribution 4.0 International License.
Authors who publish with this journal agree to the following terms:
- Authors retain copyright and grant the journal right of first publication with the work simultaneously licensed under a Creative Commons Attribution License [CC BY-NC-SA 4.0] that allows others to share the work with an acknowledgment of the work's authorship and initial publication in this journal.
- Authors are able to enter into separate, additional contractual arrangements for the non-exclusive distribution of the journal's published version of the work, with an acknowledgment of its initial publication in this journal.
- Authors are permitted and encouraged to post their work online.
