ADOMIAN DECOMPOSITION METHOD AND VARIATIONAL ITERATION METHOD FOR SOLVING SASA-SATSUMA EQUATION
DOI:
https://doi.org/10.25271/sjuoz.2025.13.3.1561Keywords:
Sasa-Satsuma Equation, Nonlinear Schrödinger Equation, Numerical Solution, Adomian Decomposition Method, Hirota-Satsuma coupled kdv systems, Sumudu Transform method.Abstract
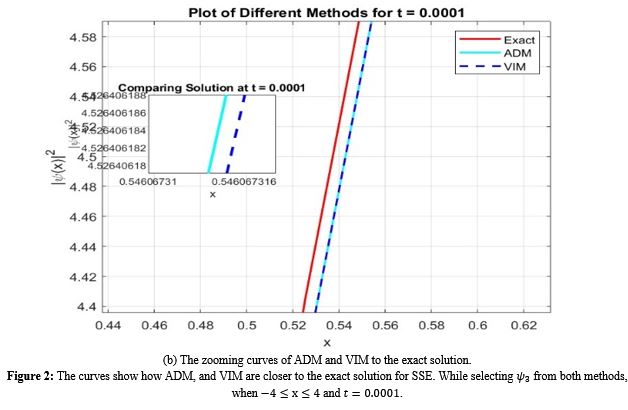
The Sasa-Satsuma equation is an integrable higher-order nonlinear Schrodinger equation. In this paper, two schemes are proposed to study numerical solutions of the Sasa-Satsuma nonlinear Schrödinger equation with initial conditions using the Adomian decomposition method and the variational iteration method. Both approaches produce quickly convergent series for each scheme with particularly important features. The present results have been displayed graphically and, in a table, to demonstrate the effectiveness and applicability of those techniques. The results obtained by the Adomian decomposition method are compared with the exact solution as well as the results obtained by variational iteration method. A comparison between the two approaches reveals that the Adomian decomposition approach is closer and more efficient than the variational iteration approach
References
Adams, C. S., & Hughes, I. (2019). Optics f2f: from Fourier to Fresnel. Oxford University Press. https://doi.org/10.1093/oso/9780198786788.003.0007
Akhmediev, N., Soto-Crespo, J. M., Devine, N., & Hoffmann, N. P. (2015). Rogue wave spectra of the Sasa–Satsuma equation. Physica D: Nonlinear Phenomena, 294, 37–42. https://doi.org/10.1016/j.physd.2014.11.006
Akram Abdulqadr, D., & Nawzad Mustafa, A. (2025). Global Stability And Hopf Bifurcation Of A Delayed Predator-Prey Model Incorporating Allee Effect And Fear Effect. 13(1), 83–88. https://doi.org/10.25271/sjuoz.2024.12.3.1406
Azzo, S. M., & Manaa, S. A. (2022). Sumudu-Decomposition Method to Solve Generalized Hirota-Satsuma Coupled Kdv System. Science Journal of University of Zakho, 10(2), 43–47. https://doi.org/10.25271/sjuoz.2022.10.2.879
Chen, Y., & An, H. L. (2008). Numerical solutions of coupled Burgers equations with time- and space-fractional derivatives. Applied Mathematics and Computation, 200(1), 87–95. https://doi.org/10.1016/j.amc.2007.10.050
Dehghan, M., & Salehi, R. (2011). The use of variational iteration method and Adomian decomposition method to solve the Eikonal equation and its application in the reconstruction problem. International Journal for Numerical Methods in Biomedical Engineering, 27(4), 524–540. https://doi.org/10.1002/cnm.1315
Duan, J.-S., Rach, R., Baleanu, D., & Wazwaz, A.-M. (2012). A review of the Adomian decomposition method and its applications to fractional differential equations. Communications in Fractional Calculus, 3(2), 73–99.
Ghorbani, A., & Saberi-Nadjafi, J. (2009). An effective modification of He’s variational iteration method. Nonlinear Analysis: Real World Applications, 10(5), 2828–2833. https://doi.org/10.1016/j.nonrwa.2008.08.008
He, J.-H. (1999). Variational iteration method-a kind of non-linear analytical technique: some examples. In International Journal of Non-Linear Mechanics 34(4), 699-708. https://doi.org/10.1016/S0020-7462(98)00048-1
Hesameddini, E., & Fotros, F. (2012). Solution for Time-Fractional Coupled Klein-Gordon Schrodinger Equation Using Decomposition Method. In International Mathematical Forum 7(21) 1047-1056.
Kivshar, Y. S., & Agrawal, G. P. (2003). Optical solitons: from fibers to photonic crystals. Academic press. https://doi.org/10.1016/B978-0-12-410590-4.X5000-1
Kumar, A., & Malik, M. (2023). IMPACT OF HUNTING COOPERATION AND FEEDBACK CONTROL FOR A NONLINEAR HYBRID LESLIE–GOWER PREDATOR-PREY SYSTEM ON NONUNIFORM TIME DOMAIN. Rocky Mountain Journal of Mathematics, 53(2), 485–515. https://doi.org/10.1216/rmj.2023.53.485
Li, C., Chen, L., & Li, G. (2020). Optical solitons of space-time fractional Sasa-Satsuma equation by F-expansion method. Optik, 224, 165527. https://doi.org/10.1016/j.ijleo.2020.165527
Manaa, S. A., Easif, F. H., & Yousif, M. A. (2014). Adomian Decomposition Method for Solving the Kuramoto-Sivashinsky Equation. In IOSR Journal of Mathematics 10(1), 08-12. https://doi.org/ 10.9790/5728-10110812
Murad, M. A. S., Hamasalh, F. K., Arnous, A. H., Malik, S., Iqbal, M., & Nofal, T. A. (2024). Optical solitons with conformable fractional evolution for the (3+1)-dimensional Sasa–Satsuma equation. Optical and Quantum Electronics, 56(10), 1733. https://doi.org/10.1007/s11082-024-07617-8
Murad, M. A. S., Hamasalh, F. K., & Ismael, H. F. (2024). Time-fractional Chen-Lee-Liu equation: Various optical solutions arising in optical fiber. Journal of Nonlinear Optical Physics and Materials, 33(6), 2350061. https://doi.org/10.1142/S0218863523500613
Odibat, Z. M., & Momani, S. (2006). Application of Variational Iteration Method to Nonlinear Differential Equations of Fractional Order. In International Journal of Nonlinear Sciences and Numerical Simulation 7(1), 27-34. https:// doi.org/10.1515/IJNSNS.2006.7.1.27
Ray, S. S., & Bera, R. K. (2005). Analytical solution of the Bagley Torvik equation by Adomian decomposition method. Applied Mathematics and Computation, 168(1), 398–410. https://doi.org/10.1016/j.amc.2004.09.006
Sabali, A. J., Manaa, S. A., & Easif, F. H. (2018). Adomian and Adomian-Padé Technique for Solving Variable Coefficient Variant Boussinesq System. Science Journal of University of Zakho, 6(3), 108–112. https://doi.org/10.25271/sjuoz.2018.6.3.514
Sabali, A. J., Manaa, S. A., & Easif, F. H. (2021). New Successive Approximation Methods for Solving Strongly Nonlinear Jaulent-Miodek Equations. Science Journal of University of Zakho, 9(4), 193–197. https://doi.org/10.25271/sjuoz.2021.9.4.869
Sadigh Behzadi, S. (2011). SOLVING SCHR¨ODINGERSCHR¨ SCHR¨ODINGER EQUATION BY USING MODIFIED VARIATIONAL ITERATION AND HOMOTOPY ANALYSIS METHODS. In Journal of Applied Analysis and Computation 1 (4), 427-437. https://doi.org/10.11948/2011029
Sasa, N., & Satsuma, J. (1991). New-type of soliton solutions for a higher-order nonlinear Schrödinger equation. Journal of the Physical Society of Japan, 60(2), 409–417. https://doi.org/10.1143/JPSJ.60.409
Sweilam, N. H., & Al-Bar, R. F. (2007). Variational iteration method for coupled nonlinear Schrödinger equations. Computers and Mathematics with Applications, 54(7–8), 993–999. https://doi.org/10.1016/j.camwa.2006.12.068
Tatari, M., Dehghan, M., & Razzaghi, M. (2007). Application of the Adomian decomposition method for the Fokker-Planck equation. Mathematical and Computer Modelling, 45(5–6), 639–650. https://doi.org/10.1016/j.mcm.2006.07.010
Tatari, M., Haghighi, M., & Dehghan, M. (2011). Adomian Decomposition and Variational Iteration Methods for Solving a Problem Arising in Modelling of Biological Species Living Together. In Z. Naturforsch 66(1-2), 93-105. http://znaturforsch.com
Wazwaz, A. M., & Kaur, L. (2019). Optical solitons and Peregrine solitons for nonlinear Schrödinger equation by variational iteration method. Optik, 179, 804–809. https://doi.org/10.1016/j.ijleo.2018.11.004
Wu, C., Zhang, G., Shi, C., & Feng, B.-F. (2022). General rogue wave solutions to the Sasa-Satsuma equation. arXiv preprint arXiv:2206.02210. http://arxiv.org/abs/2206.02210
Wu, J. P., & Geng, X. G. (2017). Inverse scattering transform of the coupled sasa-satsuma equation by riemann-hilbert approach. Communications in Theoretical Physics, 67(5), 527–534. https://doi.org/10.1088/0253-6102/67/5/527
Published
How to Cite
Issue
Section
License
Copyright (c) 2025 Knier A. Salih, Saad A. Manaa
This work is licensed under a Creative Commons Attribution 4.0 International License.
Authors who publish with this journal agree to the following terms:
- Authors retain copyright and grant the journal right of first publication with the work simultaneously licensed under a Creative Commons Attribution License [CC BY-NC-SA 4.0] that allows others to share the work with an acknowledgment of the work's authorship and initial publication in this journal.
- Authors are able to enter into separate, additional contractual arrangements for the non-exclusive distribution of the journal's published version of the work, with an acknowledgment of its initial publication in this journal.
- Authors are permitted and encouraged to post their work online.
